Mathematics

Introduction

The Mathematics Department aims to enthuse and empower students to learn and use mathematics in future engagements. We seek to develop confident and competent, self-directed learners and users of mathematical problem solving in the 21st Century.

Student Outcomes

The Additional Mathematics Syllabus aims to enable students who have an aptitude and interest in mathematics to:

• Acquire mathematical concepts and skills for higher studies in mathematics and to support learning in the other subjects, in particular, the sciences;

• Develop thinking, reasoning and meta-cognitive skills through a mathematical approach to problem-solving;

• Connect ideas within mathematics and between mathematics and the sciences through applications of mathematics; and

• Appreciate the abstract nature and power of mathematics.

The Mathematics Syllabus aims to enable all students to:

• Acquire mathematical concepts and skills for continuous learning in mathematics and to support learning in other subjects;
• Develop thinking, reasoning, communication, application and metacognitive skills through a mathematical approach to problem-solving; 
• Connect ideas within mathematics and between mathematics and other subjects through applications of mathematics; 
• Build confidence and foster interest in mathematics.

The N(T) Mathematics Syllabus aims to enable students who are bound for post-secondary vocational education to:

• Acquire mathematical concepts and skills for real life, to support learning in other subjects, and to prepare for vocational education; 

• Develop thinking, reasoning, communication, application and metacognitive skills through a mathematical approach to problem solving; and 

• Build confidence in using mathematics and appreciate its value in making informed decisions in real life.

Mathematics Learning Journeys & Learning Experiences

In our effort towards student-centric, values-driven education, we want to nurture engaged learners who are motivated and enjoy learning. One of the areas to make every student an engaged learner is to ignite the joy of learning. This can be achieved in many means. We chose Experiential Learning.

Learning Journeys and Learning Experiences are designed for students to have the opportunities to apply knowledge and skills learnt in class in real-life contexts. We have evolved to integrate more subjects into these learning journeys.

Through these learning experiences, our students learn to realise the relevance of their lessons in school and have developed renewed enthusiasm and drive to greater achievement in school. Through this all, our students see meaningful learning of Mathematics and Problem solving in the real world.

Singapore Mathematical Olympiad (SMO) Competition 2025 We wish to extend our warmest congratulations to all the students who represented our school in the Singapore Mathematical Olympiad (SMO) 2025. This prestigious national competition, organised by the Singapore Mathematical Society (SMS), is designed to challenge the ingenuity and mathematical problem-solving ability of Singapore’s most talented students.

Our students’ dedication and intellectual rigor were evident during the competition , and we are incredibly proud of every participant. Special recognition goes to the following students for their outstanding performance:

Junior Section

• Peng Ruoqi (Honourable Mention)

Senior Section

• Yong Zhi Xuan (Bronze Award)
• Alex Sng (Sun Yaoyang) (Participation)
• Bong Qi Ern (Participation)
• Emma Lim Hui Ting (Participation)

Well done to all for pushing the boundaries of their mathematical potential!

Learning Journey to Sports Hub Museum Our BDSians had an engaging hands-on learning experience as they applied mathematical concepts to real-world sports scenarios at the Sports Hub Museum. The learning journey began with students measuring their brisk walking times and calculating their speeds, comparing their results to professional athletes by using percentage differences and ratio calculations. This practical approach allowed them to understand how math can be used to measure and evaluate performance in sports.

Next, using a floorball stick, the students participated in an activity to measure the ratio of successful attempts, providing them with a deeper understanding of probability and the significance of repeated trials in sports. By applying these mathematical principles, they not only gained insight into how athletes measure their own performance but also explored the concept of consistency and how it impacts overall success in sports.

The experience didn’t stop there; students also engaged in mathematical investigations where they analysed historical sports data to identify trends and patterns in athletic performance. They examined how various factors, such as training techniques and advancements in equipment, have contributed to improvements in performance over time. By visualising their findings through graphs and charts, they learned how to interpret data in a way that can drive conclusions and inform decision-making in sports science.

This interactive and multi-faceted approach not only made learning math fun but also demonstrated the crucial role mathematics plays in understanding and advancing sports performance. Students saw firsthand how mathematical skills are essential tools in analysing, improving, and optimizing athletic abilities, while also reinforcing teamwork, critical thinking, and data analysis skills.

Learning Journey to URA Centre Our Secondary 3NT students embarked on an enlightening Learning Journey to the Urban Redevelopment Authority (URA) of Singapore, immersing themselves in a lesson enriched with map scales, statistical diagrams, population comparisons, and 3D objects.

Engaging in hands-on activities, they skillfully wielded the ‘Measure’ app on their iPads and interacted with dynamic displays, unraveling the complexities of map representation and scale manipulation.

Leveraging on the use of Classkick, students instantly verified their answers and received constructive feedback, enhancing their methodological prowess. This immersive educational experience bestows upon them not just mathematical proficiency but also a profound appreciation for the practical applications of Mathematics in the real world.

Learning Experience on Probability

Learning Experience on Pythagoras Theorem using Digital Escape Room

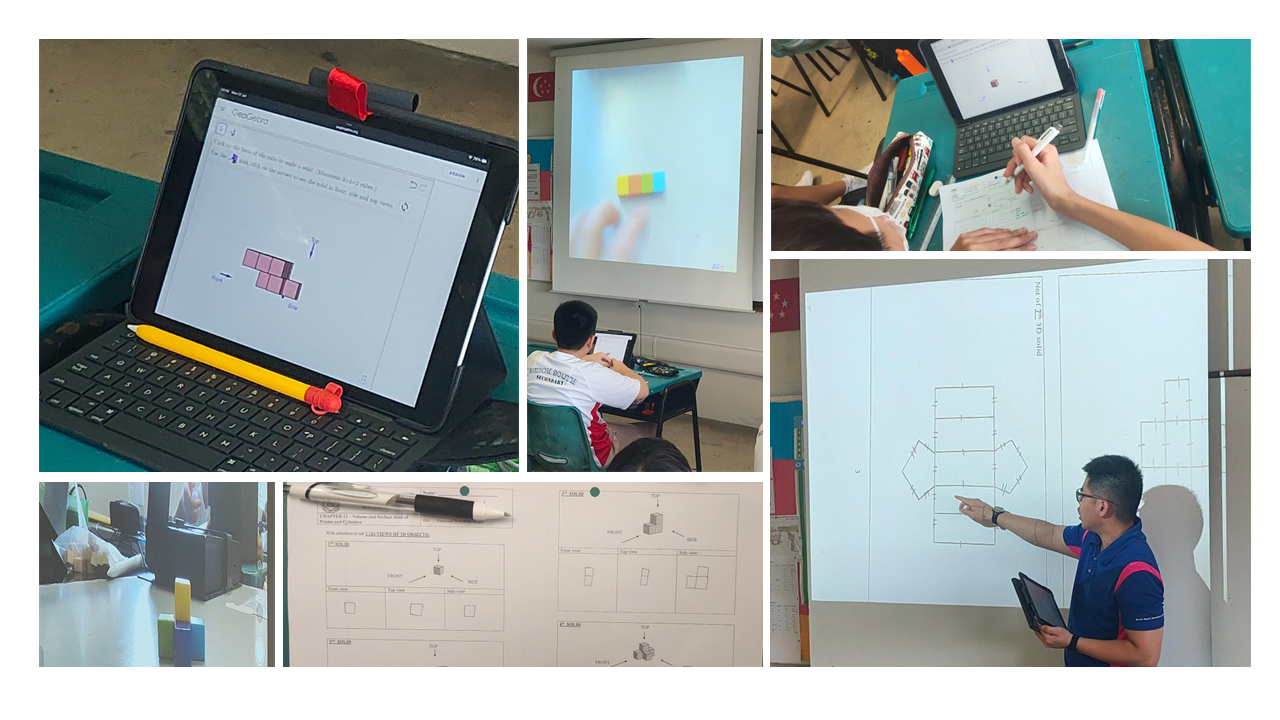
Learning Experience on Nets of Solid Shapes using CoSpaces Edu

Learning Experience on Surface Area of Sphere

ICAN

In reaching out to the under-achievers in a Mathematics class, the ICAN principles were adopted this year in the Normal Technical and Normal Academic classes to better meet these students’ needs.

Using the 8 Principles as a guide, the teacher carefully designs his/ her teaching package to deliver a more effective lesson. The lesson may comprise of good learning experiences such as the use of manipulatives and focus on a real-life context. 

The unique feature of the ICAN framework is the mentoring aspect. The mentor who is assigned to the teacher will provide feedback on the lesson design, sits in for the lesson observation and conducts the post lesson conference. During the post lesson conference, students’ learning gaps or misconceptions that were observed would be discussed further. 

Although this project requires massive manpower and careful deployment, it has been worthwhile as both the teachers and students have benefitted much from it. 

Students’ feedback on the lessons was encouraging while teachers felt that they became more reflective and effective in delivering a good lesson.